‘Great ratios’ in economics don’t all add up

The idea that certain economic ratios are roughly constant in the long run is an old one. Nicholas Kaldor (“A Model of Economic Growth”) described them as “stylized facts;” L.R. Klein and R.F. Kosobud (“Some Econometrics of Growth: Great Ratios of Economics”) labeled them “great ratios.”

Such ratios are widely adopted in theoretical models in economics as conditions for balanced growth, arbitrage or solvency. However, the empirical literature has tended to find little evidence for them. Using novel estimation methods and a dataset spanning almost one and a half centuries and 17 countries, we find support for five out of seven great ratios.

Great ratios in economics

Kaldor wrote: “A satisfactory model concerning the nature of the growth process in a capitalist economy must also account for the remarkable historical constancies revealed by recent empirical investigations.”

He further noted that output per worker and capital per worker have grown at similar rates, so the capital/output ratio was roughly constant as the relationship between the share of wages in national income and the return on capital.

Klein and Kosobud also considered the savings–income ratio, the velocity of money in circulation, capital per worker and the labor force participation rate. While there was some skepticism about these stylized facts—Robert Solow in his classic book, Growth Theory, commented that there “is no doubt that they are stylized, though it is possible to question whether they are facts”—they were widely adopted in theoretical models of economic growth as well as in models of business cycles.

Stable ratios are implied by a range of economic theories about the conditions required for balanced growth, arbitrage or solvency and are equivalent to a unit, long-run coefficient (equal to the number 1) associated with the ratio—the combination of the denominator and the numerator that each change at the same rate over the long run.

Stability has also often been interpreted in terms of the statistical definition of being stationary, rather than possessing stochastic (randomly determined) trends. A stable ratio is interpreted as being the case where the logarithms of two variables, say x and y, feature a stochastic trend, but their difference, x-y, does not and is stationary. In the language of econometrics, the variables are said to be co-integrated with a unit, long-run coefficient.

In our recent paper, we investigate seven great ratios. We consider two balanced growth conditions: 1) the logarithms of consumption and gross domestic product (GDP); 2) the logarithms of investment and GDP. We look at two solvency conditions: 3) the logarithms of imports and exports; 4) the logarithms of public debt and GDP.

We consider a term structure relationship: 5) short and long interest rates, arbitrage and expectations that should stop them from diverging. We look at the Fisher effect that theoretically ties 6) inflation and long interest rates. And, finally, we consider a velocity equation between 7) inflation and money growth.

Strictly speaking, the last three are not ratios but their long-run constancy (long-run unit coefficient) is often assumed in economics.

Empirical evidence on great ratios

The stability of the great ratios has prompted a large empirical literature. It tends to find little evidence for the stability of the great ratios. As Dan Harding notes in “Econometric Foundations of the Great Ratios of Economics,” … econometric tests reject the great ratios hypothesis but economic growth theorists and quantitative macroeconomic model builders continue to embed that hypothesis in their work.”

However, all economic hypotheses are joint hypotheses, involving both the substantive hypothesis of interest, for instance that the ratio is stable, and a set of auxiliary choices required to make the substantive hypothesis operational.

It is therefore possible that a rejection could arise because of the auxiliary choices, even if the hypothesis of interest is true. These auxiliary choices include how to measure the variables, how to choose the sample and how to conduct estimation and inference. For example, series like the pound sterling/dollar real exchange rate, which seem to feature a stochastic trend over short spans, appear stationary over long spans.

Estimates of the long-run coefficients

We suggest that a possible reason for the lack of existing evidence for stable ratios is that there may be intermittent failures of the adjustment mechanisms that return the variables to their equilibrium relationship.

These failures may be associated with major shocks such as wars, depressions and pandemics. This process, which we call episodic co-integration, makes it difficult to estimate the long-run coefficient with any precision from the relatively short-span time series for a single country typically used.

To investigate this issue, we take advantage of the long-span data, 1870–2016, for a panel of 17 countries that became available in the Jordá-Schularick-Taylor Macrohistory Database.

Using these panel data to estimate great ratios, we argue that there appears to be no approach in the existing literature that would jointly deal with episodic co-integration and other important features of this dataset, such as the intrinsic dependence across countries that arises from international economic and financial linkages and spillovers.

We propose a novel estimation method that allows for the intermittent failures of long-run adjustment mechanisms as well as other important features commonly present in international macroeconomic data, including heterogenous (country-specific) short-run dynamic behaviors and the dependence of economic variables across countries.

Chart 1 provides long-run coefficient estimates for seven variable pairs together with 95 percent statistical-confidence intervals (showing a range of possible outcomes considered statistically likely with a probability of 95 percent).

Downloadable chart | Chart data

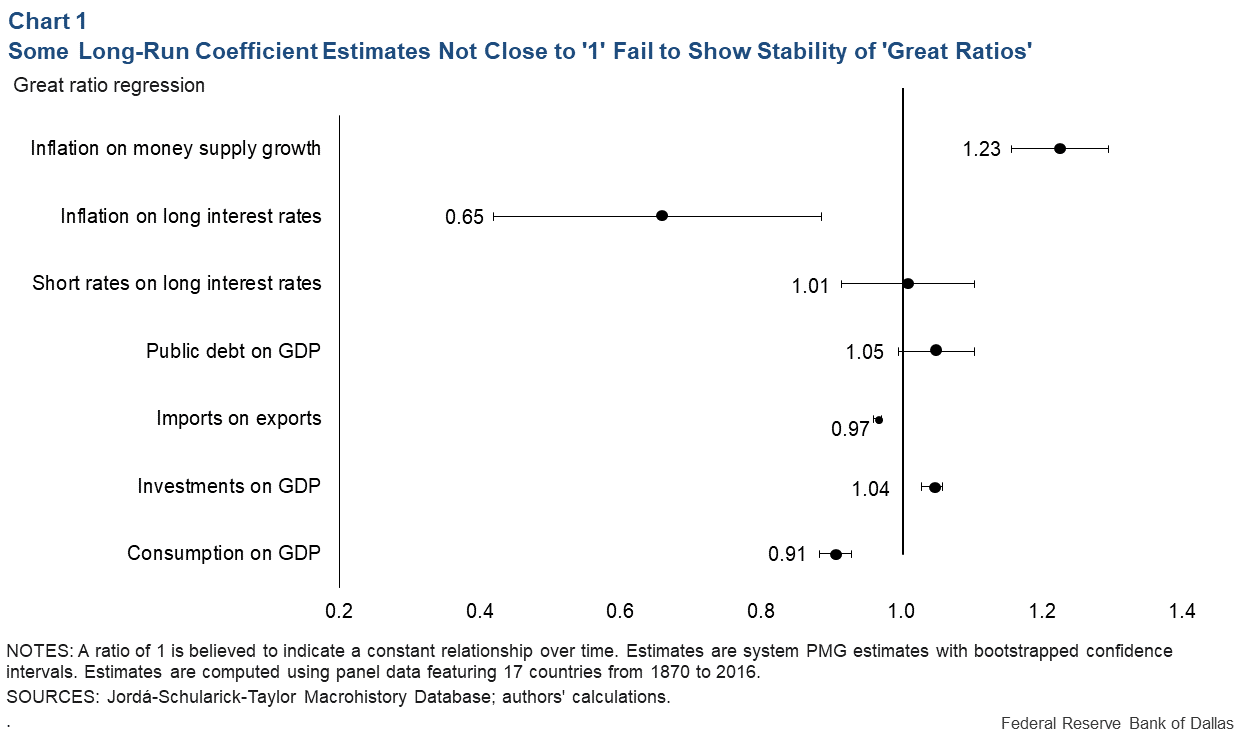
These estimates provide support for four great ratios. For public debt/GDP and long/short interest rates, the estimated long-run coefficients are close to unity and not significantly different from it statistically. For investment/GDP and imports/exports, the long-run coefficients are very close to unity but precisely estimated, suggesting they differ from 1.0 statistically.

But with such a large number of observations and quite small confidence intervals, in these two cases, it is unclear that traditional statistical-significance testing is the appropriate criteria for judging closeness to unity. From an economics perspective, they are very close. The consumption/GDP long-run coefficient is a bit further away from 1.0, estimated at 0.91 with a tight confidence interval (0.88–0.93).

We find strong evidence against two variable-pairs: Inflation/money growth, with a long-run coefficient of 1.23 that exceeds 1.0 by a large margin, and inflation/long-term interest rates, with a long-run coefficient of 0.65 that is well below 1.0.

Interpreting these estimates is a matter of judgment. A believer in the great ratios might say that five of the seven estimates of long-run coefficients—including the most important ones for growth and solvency—lie in a narrow range around 1.0. A nonbeliever might say that only two were not significantly different from 1.0.